前言

在算法竞赛中，I/O有时是影响效率的瓶颈。I/O优化可以被模板化，与具体问题无关，是常数优化的重要方式之一。看到网上有很多关于这方面的文章，我也想来自己研究一下。

NOI系列目前支持的语言有C，C++和Pascal，其中C++可以直接使用C的绝大多数功能（但也有例外），因此下面只考虑C++和Pascal两种语言。通常，每种语言都提供了几种平台无关的I/O方式，如C++中的scanf/printf，cin/cout，fread/fwrite，Pascal中的read/write，blockread/blockwrite。也有一些低级的平台有关的I/O方式，Windows和Linux(Unix)都提供了内存映射文件，效率更加高。

在算法竞赛中，I/O通常用文本文件，而数据只有整数、浮点数和字符串三种。把十进制的字符串转换成整数或浮点数需要一定的时间，而分离出字符串也需要一定的时间，这就是I/O优化的方向。我们通常优化了时间，但是也降低了通用性。

实验环境

为了保证通用性，我尽可能多的寻找平台测试。下面列举了所有用于实验的平台参数：

编号	操作系统	GCC版本	FPC版本
1(HOME)	Windows 10 x64	7.1.0	3.0.2
2(HOME)	ubuntu 14.04(NOI Linux) x86	4.8.4	2.6.2
3(SCHOOL)	Windows 7 x64	7.1.0	2.6.2
4(HOME)	Bash on Ubuntu on Windows(16.04)	5.4.0	3.0.0

整数的I/O

整数是算法竞赛中最常见的数据类型，大部分选手也只会写整数的I/O优化。下面列举进行的实验：

输入$N$个整数，输出和，用于计算输入效率
输入$N$个整数，输出这$N$个数，用空格间隔，可以计算输出效率
输入$N$个整数，输出这$N$个数，用换行符间隔，计算另一种输出效率

注意task2和task3的区别，在很多题目中要求task3。

数据生成

#include <fstream>
#include <ctime>
#include <random>
using namespace std;
ofstream fout("integer.in");
const int n = 1e7;
int main()
{
	minstd_rand gen(time(NULL));
	fout << n << endl;
	for (int i = 1; i <= n; i++)
	{
		uniform_int_distribution<> d(numeric_limits<int>::min(), numeric_limits<int>::max());
		fout << d(gen) << ' ';
	}
	fout << endl;
	return 0;
}

如果没有说明，数据规模均为$N=10^7$个整数。

系统I/O

C++的流

重定向的cin/cout

使用流来输入输出是C++的优点，有的选手采用这种用freopen重定向后，再使用cin/cout的方式。

#include <iostream>
#include <cstdio>
using namespace std;
int main()
{
	freopen("integer.in", "r", stdin);
	freopen("integer.out", "w", stdout);
	int n;
	cin >> n;
	long long sum = 0;
	for (int i = 1; i <= n; i++)
	{
		int x;
		cin >> x;
		sum += x;
	}
	cout << sum << endl;
	return 0;
}

编号	task1	task2	task3
1	11,608ms	18,968ms	19,053ms
2	4,964ms	16,807ms	17,362ms
3

注意，task2和task3都已经减掉了task1的时间。可以发现，同等规模下输出比输入慢不少。

重定向的cin/cout+关同步

很多地方都有cin/cout关同步来加速。

#include <iostream>
#include <cstdio>
using namespace std;
int main()
{
	freopen("integer.in", "r", stdin);
	freopen("integer.out", "w", stdout);
	ios::sync_with_stdio(false);
	int n;
	cin >> n;
	long long sum = 0;
	for (int i = 1; i <= n; i++)
	{
		int x;
		cin >> x;
		sum += x;
	}
	cout << sum << endl;
	return 0;
}

编号	task1	task2	task3
1	2,266ms	18,854ms	18,527ms
2	1,274ms	16,772ms	16,840ms
3

这次更加明显，输入比输出快8倍以上。关同步有效地加快了输入，但对于输出并没有效果。

文件流

文件流是C++中最适合处理文件输入输出的方式，但用的人并不多。

#include <fstream>
using namespace std;
ifstream fin("integer.in");
ofstream fout("integer.out");
int main()
{
	int n;
	fin >> n;
	long long sum = 0;
	for (int i = 1; i <= n; i++)
	{
		int x;
		fin >> x;
		sum += x;
	}
	fout << sum << endl;
	return 0;
}

编号	task1	task2	task3
1	2,172ms	1,826ms	18,639ms
2	1,187ms	1,129ms	16,374ms
3

文件流在task1上基本与上一种方法一样，但是task2快了10倍，task3和前面的一样慢。然而，把std::endl改成’\n’之后，task3就和task2一样快了。这是因为调用std::endl会执行flush操作。

C风格的格式化I/O

用freopen重定向，并使用scanf/printf进行格式化输入输出。

#include <cstdio>
int main()
{
	freopen("integer.in", "r", stdin);
	freopen("integer.out", "w", stdout);
	int n;
	scanf("%d", &n);
	long long sum = 0;
	for (int i = 1; i <= n; i++)
	{
		int x;
		scanf("%d", &x);
		sum += x;
	}
	printf("%lld\n", sum);
	return 0;
}

编号	task1	task2	task3
1	8,234ms	3,187ms	3,261ms
2	1,171ms	1,137ms	1,163ms
3

Pascal的read/write

Program IOtest;

Var 
  n,i,x: longint;
  sum: int64;
Begin
  assign(input,'integer.in');
  reset(input);
  assign(output,'integer.out');
  rewrite(output);
  read(n);
  sum := 0;
  For i:=1 To n Do
    Begin
      read(x);
      inc(sum,x);
    End;
  writeln(sum);
  close(input);
  close(output);
End.

编号	task1	task2	task3
1	2,361ms	2,490ms	2,499ms
2	1,495ms	1,502ms	1,592ms
3

Pascal的I/O比文件流稍慢一些，但还是很快的。

总结

系统I/O的速度与平台有很大的关系，所以我们要尽可能多找实验平台测试。在我家里的Windows下的结果如下：

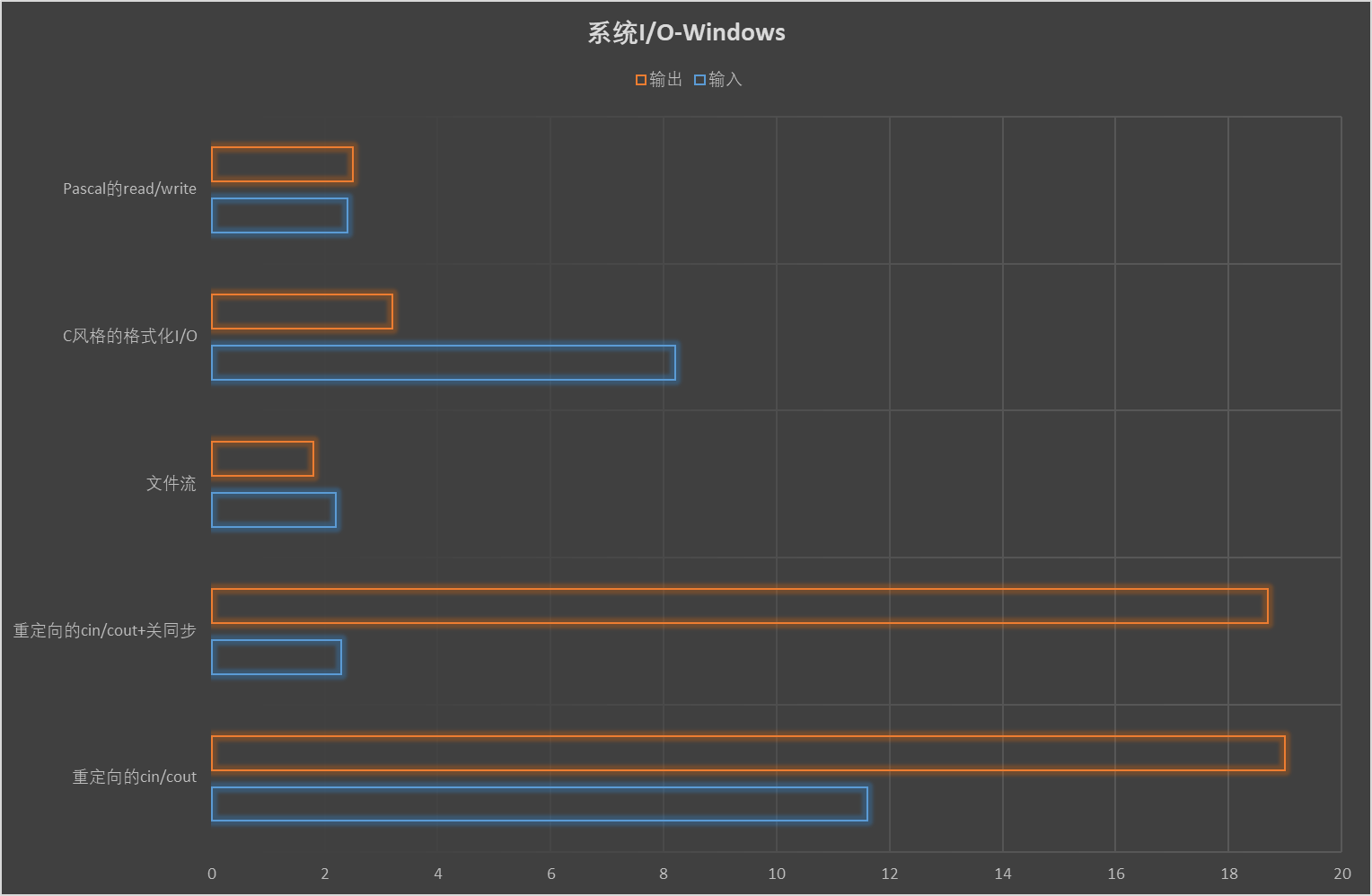
I/O优化

I/O优化以牺牲通用性为代价来提高效率，在OI中很常用。其核心思想是：利用一个逐字符输入/输出函数，手动实现字符与整数的转化，也就是十进制与二进制的转化。系统I/O要考虑各种特殊情况，所以效率低下。下面的这段代码使用scanf输入字符串，再用atoi把字符串转为整数，但是比直接用scanf快一些，就体现了上述内容。这可以算是原始的输入优化。

#include <cstdio>
#include <cstdlib>
int main()
{
	freopen("integer.in", "r", stdin);
	freopen("integer.out", "w", stdout);
	int n;
	scanf("%d", &n);
	long long sum = 0;
	for (int i = 1; i <= n; i++)
	{
		char buf[20];
		scanf("%s", buf);
		sum += atoi(buf);
	}
	printf("%lld\n", sum);
	return 0;
}

普通I/O优化

基于最近一次模拟赛的代码，下面是大部分人用的输入优化模板，但是没有输出优化。于是我使用了szb’s version。

inline int read()
{
	int k = 0, f = 1;
	char ch = getchar();
	while (ch < '0' || ch > '9')
	{
		if (ch == '-')
			f = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9')
	{
		k = k * 10 + ch - '0';
		ch = getchar();
	}
	return k * f;
}
inline void write(int x)
{
	if (x < 0)
		putchar('-'), x = -x;
	if (x >= 10)
		write(x / 10);
	putchar(x % 10 + '0');
}
inline void writeln(int x)
{
	write(x);
	puts("");
}

编号	task1	task2	task3
1	2,983ms	3,188ms	3,438ms
2
3

基于fread/fwrite的I/O优化

本来想用别人的，但发现没有写输出优化，于是上我自己在模拟赛时写的最新版本。

#include <cstdio>
#include <cctype>
FILE *fin = fopen("integer.in", "r"), *fout = fopen("integer.out", "w");
const int SZ = 1e6;
char buf[SZ], *p = buf, *pend = buf;
inline int nextchar()
{
	if (p == pend)
	{
		pend = (p = buf) + fread(buf, 1, SZ, fin);
		if (pend == buf)
			return EOF;
	}
	return *p++;
}
template <typename Int>
inline void read(Int &x)
{
	char c = nextchar();
	for (; isspace(c); c = nextchar())
		;
	x = 0;
	Int sign = 1;
	if (c == '-')
	{
		sign = -1;
		c = nextchar();
	}
	for (; isdigit(c); c = nextchar())
		x = x * 10 + c - '0';
	x *= sign;
}
inline void writechar(char c)
{
	if (p == pend)
	{
		fwrite(buf, 1, SZ, fout);
		p = buf;
	}
	*p++ = c;
}
inline void flush()
{
	fwrite(buf, 1, p - buf, fout);
}
int dig[20];
template <typename Int>
inline void writeln(Int x)
{
	if (x < 0)
	{
		writechar('-');
		x = -x;
	}
	int len = 0;
	do
		dig[++len] = x % 10;
	while (x /= 10);
	for (; len; len--)
		writechar(dig[len] + '0');
	writechar('\n');
}
int main()
{
	int n;
	read(n);
	long long sum = 0;
	for (int i = 1; i <= n; i++)
	{
		int x;
		read(x);
		sum += x;
	}
	writeln(sum);
	flush();
	return 0;
}

编号	task1	task2	task3
1	296ms	485ms	609ms
2
3

探究算法竞赛中的输入输出效率

前言